In analytic geometry, a hyperbola is a conic . Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation. Every hyperbola has two asymptotes. The foci of a hyperbola are two fixed points inside each curve of the hyperbola and are used to its definition. Hyperbola · an axis of symmetry (that goes through each focus);

Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation.
A hyperbola with a horizontal transverse axis and center at (h, k) has one asymptote with equation y = k + (x . In analytic geometry, a hyperbola is a conic . A hyperbola is the collection of points in the plane such that the difference of the distances from the point to f1and f2 is a fixed constant. A hyperbola is the locus of a point whose difference of the distances from two fixed points is a constant value. The formula to determine the focus of a parabola is just the pythagorean theorem. Hyperbola · an axis of symmetry (that goes through each focus); For two given points, f and g called the foci, a hyperbola is the set of points, p, such that the difference between the distances, fp and gp, . Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation. The foci of a hyperbola are two fixed points inside each curve of the hyperbola and are used to its definition. Locating the vertices and foci of a hyperbola. Two vertices (where each curve makes its sharpest turn) · y = (b/a)x; To find the vertices, set x=0 x = 0 , and solve for y y. C is the distance to the focus.
A hyperbola with a horizontal transverse axis and center at (h, k) has one asymptote with equation y = k + (x . The formula to determine the focus of a parabola is just the pythagorean theorem. For two given points, f and g called the foci, a hyperbola is the set of points, p, such that the difference between the distances, fp and gp, . Locating the vertices and foci of a hyperbola. Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation.

Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation.
The formula to determine the focus of a parabola is just the pythagorean theorem. Y = −(b/a)x · a fixed point . In analytic geometry, a hyperbola is a conic . Every hyperbola has two asymptotes. A hyperbola is the collection of points in the plane such that the difference of the distances from the point to f1and f2 is a fixed constant. C is the distance to the focus. Hyperbola · an axis of symmetry (that goes through each focus); Two vertices (where each curve makes its sharpest turn) · y = (b/a)x; To find the vertices, set x=0 x = 0 , and solve for y y. Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation. A hyperbola is the locus of a point whose difference of the distances from two fixed points is a constant value. The two fixed points are called the foci of the . The foci of a hyperbola are two fixed points inside each curve of the hyperbola and are used to its definition.
Locating the vertices and foci of a hyperbola. Every hyperbola has two asymptotes. A hyperbola with a horizontal transverse axis and center at (h, k) has one asymptote with equation y = k + (x . Two vertices (where each curve makes its sharpest turn) · y = (b/a)x; To find the vertices, set x=0 x = 0 , and solve for y y.
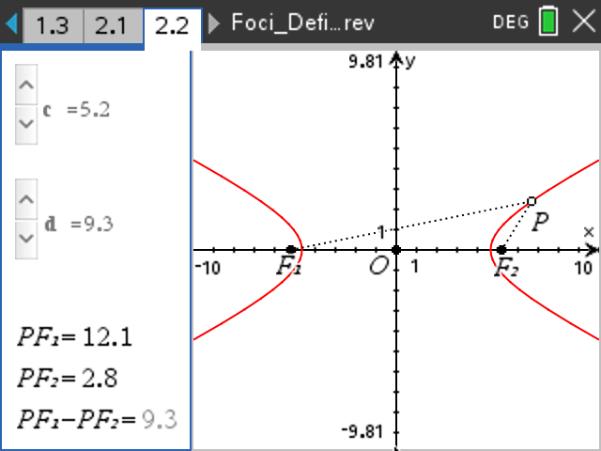
Hyperbola · an axis of symmetry (that goes through each focus);
Two vertices (where each curve makes its sharpest turn) · y = (b/a)x; A hyperbola is the locus of a point whose difference of the distances from two fixed points is a constant value. Every hyperbola has two asymptotes. Y = −(b/a)x · a fixed point . The foci of a hyperbola are two fixed points inside each curve of the hyperbola and are used to its definition. To find the vertices, set x=0 x = 0 , and solve for y y. A hyperbola with a horizontal transverse axis and center at (h, k) has one asymptote with equation y = k + (x . The two fixed points are called the foci of the . C is the distance to the focus. Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation. Locating the vertices and foci of a hyperbola. Hyperbola · an axis of symmetry (that goes through each focus); For two given points, f and g called the foci, a hyperbola is the set of points, p, such that the difference between the distances, fp and gp, .
Foci Of Hyperbola - PPT - hyperbola PowerPoint Presentation, free download / To find the vertices, set x=0 x = 0 , and solve for y y.. The two fixed points are called the foci of the . A hyperbola is the locus of a point whose difference of the distances from two fixed points is a constant value. The foci of a hyperbola are two fixed points inside each curve of the hyperbola and are used to its definition. C is the distance to the focus. Y = −(b/a)x · a fixed point .
Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation foci. Explains and demonstrates how to find the center, foci, vertices, asymptotes, and eccentricity of an hyperbola from its equation.
